Mengukur Volatilitas Pada Data Time Series (Model ARCH dan GARCH) di Eviews 9

Gambar : Cover Artikel 

Mengukur Volatilitas Pada Data Time Series Dengan Model ARCH dan GARCH

Ditulis oleh : Dimas Purbo Wicaksono Fenda Putra, S.E.

A.Penjelasan Volatilitas Data Time Series

Pengukuran volatilitas sangat diperlukan untuk sektor keuangan seperti saham, nilai tukar dan inflasi yang mempunyai fenomena tertentu dan biasa disebut volatility clustering (pengelompokan volatilitas). Volatility clustering adalah pengelompokan volatilitas dimana harga saham menunjukkan pengayunan lebar dan diikuti pergerakan harga yang tenang untuk periode tertentu. Di berbagai bidang ilmu seperti misal ilmu makro ekonometrika sangat memerlukan pengukuran volatilitas, karena makro ekonometrika mempelajari banyak hal termasuk variabilitas pada tingkat inflasi yang terjadi sepanjang waktu. Pada dasarnya inflasi tidaklah buruk, yang menjadikan inflasi buruk yaitu adanya variabilitas. Variabilitas menyebabkan perencanaan keuangan menjadi terhambat. Oleh karena itu, pengukuran ini biasa digunakan oleh para pengambil keputusan untuk mengantisipasi dan merencanakan keuangan dengan baik.

Tidak hanya bagi pengambil keputusan semua yang berada pada lingkaran keuangan (pasar uang) sangat membutuhkan pengukuran ini. Karena variabilitas dapat menjadikan kerugian atau bahkan bisa menghasilkan laba yang besar. Misalnya, pada investor yang berada di lingkaran pasar harga saham. Investor di lingkaran pasar harga saham sangat berkepentingan terhadap volatilitas harga saham, volatilitas harga saham yang tinggi berarti kerugian atau laba besar yang pada akhirnya dapat menjadikan ketidakpastian. Intinya, volatilitas yang tinggi dapat mempersulit perusahaan untuk memperoleh modal di dalam pasar modal.

Yang menjadi topik pembahasan di tulisan ini adalah bagaimana cara membuat perkiraan atau peramalan pada data time series yang memiliki volatilitas. Kemudian bagaimana membuat model perkiraan atau peramalan pada data time series (data apapun, seperti : inflasi dan lain sebagainya).

Sebelum masuk ke caranya kita harus mengetahui terlebih dahulu ciri dari data time series, khususnya untuk keuangan. Ciri yang mendasar pada data time series keuangan adalah memiliki susunan acak atau random walk pada bentuk level atau level form yang dapat diartikan bahwa data tidak stasioner. Lain halnya jika dalam bentuk difference pertama atau firs difference form, umumnya data stasioner. Pada dasarnya apapun statusnya, sudah stasioner ataupun belum, ketika masih memiliki volatilitas atau disini disebut "wide swing", artinya masih terdapat variasi pada data time series untuk periode waktu yang panjang.

Untuk mengetahui, pertama-tama buat model "variasi variance" atau "autoregresive conditional heteroskedasticity (ARCH)".

Pertama kita masuk ke pembahasan Autoregresive Conditional Heteroskedasticity (ARCH)

ARCH dikembangkan oleh Engle pada tahun 1982. Model ini memiliki struktur autoregressive dimana heteroskedastisity diobservasi untuk periode yang berbeda. Asumsi dari model ini yaitu bahwa variabel residual tidak konstan. Untuk memperjelas bagaimana model ARCH dibentuk, berikut adalah contoh model regresi sederhana :

Y_t = β₀ + β₁X_t + €_t

Dimana :

Yt = variabel dependent

Xt = variabel independent

£ = Residual

Di dalam model regresi di atas terjadinya heteroskedastisitas berhubungan langsung dengan variabel independent sehingga supaya model terbebas dari heteroskedastisitas maka hanya perlu transformasi persamaan regresi. Model ARCH berbeda dari asumsi tersebut. Heteroskedastisitas terjadi karena data time series menunjukkan unsur volatilitas misal nilai kurs pada satu periode volatilitasnya tinggi dan residualnya juga tinggi, diikuti suatu periode yang valatilitasnya rendah dan nilai residualnya juga rendah. Dengan kondisi ini maka variance residual dari model akan sangat tergantung dari volatilitas residual periode sebelumnya.

a.Mendeteksi unsur ARCH

Data time series diduga seringkali mengandung masalah autokorelasi, sedangkan data cross section diduga mengandung masalah heteroskedastisitas. Engle menunjukkan bahwa seringkali data time series selain mengandung masalah autokorelasi juga diduga mengandung masalah heteroskedastisitas. Untuk mendeteksi ada atau tidaknya unsur heteroskedastisitas di dalam data time series yaitu mengetahui pola residual kuadrat dari Correlogram. Jika tidak ada unsur ARCH di dalam residual kuadrat maka Autocorrelation Function (ACF) dan Partial Autocorelation Function (PACF) seharusnya adalah nol pada semua kelambatan atau secara statistic tidak signifikan. Sebaliknya jika ACF dan PACF tidak sama dengan nol maka model mengandung unsur ARCH. 

Uji ada atau tidaknya unsur ARCH dalam residual kuadrat dapat juga dianalisis melalui uji statistic Ljung-Box. Jika nilai statistik L-Jung-Box lebih kecil dari nilai kritis tabel Chi Square (atau tidak signifikan), maka residual menunjukkan tidak adanya unsur ARCH. Sebaliknya jika signifikan maka residual mengandung unsur ARCH.

B.Tahapan Pengolahan Data

Berikut adalah contoh pengujiannya dengan menggunakan data inflasi tahunan dari 2005-2018 (Yang diambil di bulan Desember untuk setiap tahunnya) (14 tahun).

Gambar : Data Latihan

Langkah 1 : Buka lembar baru eviews 9.

Gambar : Pengolah Data Eviews 9

Langkah 2 : Pada Workfile Create dibagian Workfile structure type pilih Dated - regular frequency (karena data time series). Date specification dibagian Frequency pilih Annual (karena tahunan). Start date isikan dengan 2005 (sebagai tahun awal data) dan End date isikan 2018 (sebagai tahun akhir data). Klik ok.

Gambar : Pengolah Data Eviews 9

Langkah 3 : Klik menu Quick dan pilih Empty Group (Edit Series).

Gambar : Pengolah Data Eviews 9

Langkah 4 : Copy paste data beserta variabelnya. Kemudian close.

Gambar : Pengolah Data Eviews 9

Langkah 5 : Blok pada foder inflasi, klik kanan => Open.

Gambar : Pengolah Data Eviews 9

Langkah 6 : Klik View dan pilih Graph.

Gambar : Pengolah Data Eviews 9

Langkah 7 : Disini penulis menyesuaikan dengan format tampilan eviews, jadi penulis langsung klik ok.

Gambar : Pengolah Data Eviews 9

Langkah 8 : Berikut adalah hasil dari pengujian stasioneritas dengan Graph.

Gambar : Pengolah Data Eviews 9

Interpretasi Output :

Dari hasil ini terlihat bahwa ada indikasi data stasioner, hal ini dapat dilihat dari grafik yang menunjukkan pergerakan fluktuatif (naik turun) walaupun awalnya mengalami penurunan yang cukup signifikan atau tajam.

Langkah 9 : Setelah pengujian stasioneritas dengan Graph, berikutnya pengujian stasioneritas dengan Breakpoint Unit Root Test. Klik menu View dan pilih Breakpoint Unit Root Test.

Gambar : Pengolah Data Eviews 9

Langkah 10 : Pada Breakpoint Unit Root Test dibagian Test for unit root in pilih “Level” (sebagai tingkatan pertama untuk pengujian stasioneritas). Break type pilih Innovation Outlier. Trend specification dibagian Basic pilih Intercept. Breakpoint selection pilih Dicky-Fuller min-t. Lag Length dibagian method pilih Scwarz criterion. Max Lags sesuaikan dengan format yang ada di eviews yaitu 2 dan di Additional output centang Display test and selection graphs. Klik ok. 

Gambar : Pengolah Data Eviews 9

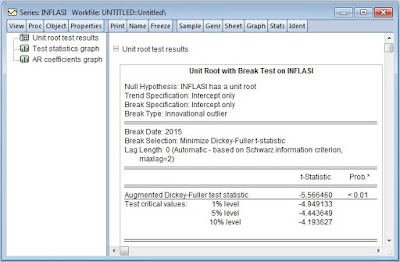
Langkah 11 : Berikut adalah hasil pengujian stasioneritas dengan Breakpoint Unit Root Test.

Gambar : Pengolah Data Eviews 9

Interpretasi Output :

Dari hasil ini dapat dilihat bahwa nilai Probabilitas Augmented Dicky Fuller test statistic sebesar 0.01 yang artinya jika dibandingkan tingkat alpha 0.05 maka lebih kecil (0.05 > 0.01) maka kesimpulannya data inflasi stasioner pada tingkatan level.

Langkah 12 : Kemudain kita mencoba membuktikannya menggunakan pengujian stasioneritas dengan correlogram. Klik menu View dan pilih Correlogram.

Gambar : Pengolah Data Eviews 9

Langkah 13 : Pada Correlogram Specification dibagian Correlogram of pilih tingkatan “level” untuk pengujian stasioneritas yang pertama. Lags to include sesuaikan dengan sistem yaitu 12 (kita bisa menyesuaikan sendiri, misal kita akan menyesuaikan dengan lags untuk Breakpoint Root Test atau disesuaikan dengan jumlah variabel). 

Gambar : Pengolah Data Eviews 9

Langkah 14 : Berikut adalah hasil dari pengujian stasioneritas dengan correlogram.

Gambar : Pengolah Data Eviews 9

Interpretasi Output :

Dari hasil output ini terlihat bawah garis line tidak ada yang keluar dari batas, artinya data stasioner. Sehingga dapat disimpulkan bahwa model inflasi tidak mengandung unsur ARCH. Kita coba buktikan apakah hasil ini sesuai jika kita mengujinya langsung ke dalam Equation Estimate. 

Langkah 15 : Kita coba dengan lags yang sama saat melakukan pengujian stasioneritas dengan Breakpoint Unit Root Test.

Gambar : Pengolah Data Eviews 9

Langkah 16 : Berikut adalah hasil dari pengujian stasioneritas dengan correlogram.

Gambar : Pengolah Data Eviews 9

Interpretasi Output :

Dari hasil output ini terlihat bawah garis line tidak ada yang keluar dari batas, artinya data stasioner. Sehingga dapat disimpulkan bahwa model untuk data inflasi tidak mengandung unsur ARCH. Kita coba buktikan apakah hasil ini sesuai jika kita mengujinya langsung ke dalam Equation Estimate. 

Langkah 17 : Klik Sheet untuk kembali menampilkan data atau dengan close hasil correlogram.

Gambar : Pengolah Data Eviews 9

Langkah 18 : Klik menu Quick dan pilih Estimate Equation.

Gambar : Pengolah Data Eviews 9

Langkah 19 : Pada Eqaution Estimation dibagian Estimation settings di Method pilih ARCH – Autoregressive Conditional Heteroskedasticity.

Gambar : Pengolah Data Eviews 9

Langkah 20 : Maka tampilannya akan seperti ini. Dibagian Mean equation yang tertulis Dependent followed by regressors & ARMA terms OR explicit equation, tuliskan inflasi c. Untuk yang lainnya sesuaikan saja dengan sistem. Klik ok.

Gambar : Pengolah Data Eviews 9

Langkah 21 : Berikut adalah hasil pengujian ARCH.

Gambar : Pengolah Data Eviews 9

Interpretasi Output :

Dari hasil ini dapat dilihat bahwa nilai Resid(-1)^2 tidak signifikan, hal ini dapat dilihat dari nilai Probabilitas yang mana nilainya sebesar 0.0975. Artinya lebih besar dari alpha 0.05 (0.05 < 0.0975). Hasil ini tidak mengindikasikan model ARCH.

Setelah membahas dan mempraktekkan mengetahui model ARCH. Berikutnya kita cari tahu Generalized Autoregresive Conditional Heteroskedasticity (GARCH).

 

b.Mendeteksi unsur GARCH

Model ARCH dari Robert Engel kemudian disempurnakan oleh Tim Bollerslev (1986) yang menyatakan bahwa variance residual tidak hanya tergantung dari residual periode lalu tetapi juga variance residual periode lalu. Jika kita memasukkan variance residual periode lalu ke persamaan maka model ini dikenal dengan Generalized Autoregresive Conditional Heteroskedasticity (GARCH). Untuk menelaskan model ARCH kita kembali menggunakan model regresi linear sederhana :

Y_t = β₀ + β₁X_t + €_t

Dimana :

Yt = variabel dependent

Xt = variabel independent

£ = Residual

Untuk penjelasan lengkapnya silakan baca buku Analisis Multivariat dan Ekonometrika Karya Prof. H.Imam Ghozali, M.Com. AK Ph.D dan Dr. Dwi Ratmono, M.Si., Ak.

C.Tahapan Pengolahan Data

Untuk memberikan contoh model GARCH kita gunakan data makro dari nilai BI Rate dari tahun 2005-2018 (14 tahun)

Gambar : Data Latihan

Langkah 1 : Buka lembar baru eviews 9.

Gambar : Pengolah Data Eviews 9

Langkah 2 : Pada Workfile Create dibagian Workfile structure type pilih Dated - regular frequency (karena data time series). Date specification dibagian Frequency pilih Annual (karena tahunan). Start date isikan dengan 2005 (sebagai tahun awal data) dan End date isikan 2018 (sebagai tahun akhir data). Klik ok.

Gambar : Pengolah Data Eviews 9

Langkah 3 : Klik menu Quick dan pilih Empty Group (Edit Series).

Gambar : Pengolah Data Eviews 9

Langkah 4 : Copy paste data beserta variabelnya. Kemudian close.

Gambar : Pengolah Data Eviews 9

Langkah 5 : Blok pada foder BI Rate, klik kanan => Open.

Gambar : Pengolah Data Eviews 9

Langkah 6 : Klik View dan pilih Graph.

Gambar : Pengolah Data Eviews 9

Langkah 7 : Disini penulis menyesuaikan dengan format tampilan eviews, jadi penulis langsung klik ok.

Gambar : Pengolah Data Eviews 9

Langkah 8 : Berikut adalah hasil dari pengujian stasioneritas dengan Graph.

Gambar : Pengolah Data Eviews 9

Interpretasi Output :

Dari hasil ini terlihat bahwa ada indikasi data stasioner, hal ini dapat dilihat dari grafik yang menunjukkan pergerakan penurunan tetapi fluktuatif (naik turun) walaupun awalnya mengalami penurunan yang cukup signifikan atau tajam.

Langkah 9 : Setelah pengujian stasioneritas dengan Graph, berikutnya pengujian stasioneritas dengan Unit Root Test. Klik menu View dan pilih Unit Root Test.

Gambar : Pengolah Data Eviews 9

Langkah 10 : Pada Unit Root Test dibagian Test type pilih Augmented Dickey-Fuller. Test for unit root in pilih “Level”. Leg Length dibagian Automatic selection pilih Schwarz Info Criterion. Maximum lags penulis sesuaikan dengan sistem yaitu 2. Include in test equation pilih Intercept. Klik ok.

Gambar : Pengolah Data Eviews 9

Langkah 11 : Berikut adalah hasil pengujian stasioneritas dengan Unit Root Test.

Gambar : Pengolah Data Eviews 9

Interpretasi Output :

Dari hasil ini dapat dilihat bahwa nilai Probabilitas Augmented Dicky Fuller test statistic sebesar 0.0394 yang artinya jika dibandingkan tingkat alpha 0.05 maka lebih kecil (0.05 > 0.0394) maka kesimpulannya data bi rate stasioner pada tingkatan level.

Langkah 12 : Kemudain kita mencoba membuktikannya menggunakan pengujian stasioneritas dengan correlogram. Klik menu View dan pilih Correlogram.

Gambar : Pengolah Data Eviews 9

Langkah 13 : Pada Correlogram Specification dibagian Correlogram of pilih tingkatan “level” untuk pengujian stasioneritas yang pertama. Lags to include sesuaikan dengan sistem yaitu 2 (kita bisa menyesuaikan sendiri, misal kita akan menyesuaikan dengan lags untuk Unit Root Test atau disesuaikan dengan jumlah variabel).

Gambar : Pengolah Data Eviews 9

Langkah 14 : Berikut adalah hasil dari pengujian stasioneritas dengan correlogram.

Gambar : Pengolah Data Eviews 9

Interpretasi Output :

Dari hasil output ini terlihat bawah garis line tidak ada yang keluar dari batas, artinya data stasioner. Sehingga dapat disimpulkan bahwa model pada data bi rate mengandung unsur GARCH. Kita coba buktikan apakah hasil ini sesuai jika kita mengujinya langsung ke dalam Equation Estimate. 

Langkah 15 : Klik menu Quick dan pilih Estimate Equation.

Gambar : Pengolah Data Eviews 9

Langkah 16 : Pada Eqaution Estimation dibagian Estimation settings di Method pilih ARCH - Autoregressive Conditional Heteroskedasticity.

Gambar : Pengolah Data Eviews 9

Langkah 17 : Maka tampilannya akan seperti ini. Dibagian Mean equation yang tertulis Dependent followed by regressors & ARMA terms OR explicit equation, tuliskan bi_rate c. Untuk yang lainnya sesuaikan saja dengan sistem. Klik ok.

Gambar : Pengolah Data Eviews 9

Langkah 18 : Berikut adalah hasil pengujian GARCH.

Gambar : Pengolah Data Eviews 9

Interpretasi Output :

Dari hasil ini dapat dilihat bahwa nilai Resid(-1)^2 tidak signifikan, hal ini dapat dilihat dari nilai Probabilitas yang mana nilainya sebesar 0.0975. Artinya lebih besar dari alpha 0.05 (0.05 < 0.0975) dan nilai GARCH (-1) signifikan yaitu sebesar 0.0013. Artinya lebih kecil dari alpha 0.05 (0.05 > 0.0013. Hasil ini mengindikasikan model GARCH.

Sebagai tambahan spesifikasi GARCH, eviews dapat mengestimasi beberapa model variasinya yang meliputi IGARCH, TARCH, EGARCH, PARCH dan component GARCH. Untuk setiap model, kita dapat dengan mudah memilihnya jika terdapat asimetri.

Informasi ekonometrika secara lengkap, silakan kunjungi channel youtube saya di : Dimas Channel

Note : Silakan bagi teman-teman yang ingin meng-copy artikel ini. Mohon sertakan sumber aslinya. Terima Kasih :-)